mapa unicesumar 2025
 |
| MAPA – SINAIS E SISTEMAS LINEARES – 52_2025 | |
| Período: | 05/05/2025 08:00 a 06/07/2025 23:59 (Horário de Brasília) |
| Status: | ABERTO |
| Nota máxima: | 3,50 |
| Gabarito: | Gabarito não está liberado! |
| Nota obtida: | |
| 1ª QUESTÃO | |||
| Mapa – Sinais e Sistemas Lineares 52/2025 A disciplina de Sinais e Sistemas Lineares está presente em diversos aspectos do nosso cotidiano. Por meio dela, é possível extrair informações da natureza — seja a partir de um sinal analógico ou digital —, processá-las e utilizá-las de forma eficiente. Um exemplo simples é a comunicação entre duas pessoas, que ocorre por meio de sinais de voz, seja em uma conversa presencial ou através de telefones e dispositivos conectados à internet. Na verdade, os sinais e sistemas estão presentes em praticamente todos os ambientes em que vivemos. No contexto da engenharia, sistemas de modulação e transmissão de sinais — como circuitos eletrônicos — são frequentemente modelados por equações diferenciais. A solução dessas equações descreve o comportamento dinâmico do sistema. Para simplificar sua resolução, utiliza-se a transformada, uma ferramenta matemática que converte equações diferenciais em equações algébricas, facilitando a análise e o projeto de circuitos. Como visto em aula, as aplicações desses conceitos são vastas, abrangendo áreas como telecomunicações, processamento de imagens, sistemas médicos e muitas outras, demonstrando a importância fundamental dos sinais e sistemas lineares na tecnologia moderna. 1) Calcule a transformada de Laplace de 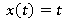 e demonstre todo o equacionamento, passo a passo.2) Calcule a transformada Z inversa do sinal  e demonstre todo o equacionamento, passo a passo.3) Calcule a transformada de Laplace do sinal 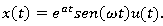 . A partir do resultado da transformada de Laplace do sinal, encontre a Função de Transferência de um sistema de malha fechada unitário (ganho =1), sendo  . |
|||
| ALTERNATIVAS | |||
|
