
mapa unicesumar 2025
 |
| ATIVIDADE 3 – CÁLCULO DIFERENCIAL E INTEGRAL II – 51_2025 | |
| Período: | 24/03/2025 08:00 a 27/04/2025 23:59 (Horário de Brasília) |
| Status: | ABERTO |
| Nota máxima: | 0,50 |
| Gabarito: | Gabarito será liberado no dia 28/04/2025 00:00 (Horário de Brasília) |
| Nota obtida: | |
| 1ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 2ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 3ª QUESTÃO | |||||||||||
| Encontre a solução geral da equação diferencial y'(x) = xy + 3x – y – 3, e assinale a alternativa correta: | |||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 4ª QUESTÃO | |||||||||||
 . |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 5ª QUESTÃO | |||||||||||
|
Uma equação diferencial linear de primeira ordem é uma das formas mais simples e fundamentais de equações diferenciais, sendo amplamente utilizada para modelar situações em que a taxa de variação de uma quantidade depende linearmente da própria quantidade. Essas equações podem ser expressas na forma geral: y′(x)+P(x)y(x) = Q(x)
em que y′(x) é a derivada da função desconhecida y(x), e P(x) e Q(x) são funções conhecidas de x. O objetivo é encontrar a função y(x) que satisfaça essa relação. Com base no excerto apresentado, encontre o valor da constante c do problema de valor inicial dado pela equação y'(x) + (1/x)*y(x) = x – 1 e condição inicial y(1) = 1: |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 6ª QUESTÃO | |||||||||||
| Encontre a solução geral da equação diferencial (x2 + y)dx + (x – 2y)dy = 0, e assinale a alternativa correta: | |||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 7ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 8ª QUESTÃO | |||||||||||
| Em um ponto (x,y,z) do espaço, a interpretação física do rotacional do campo vetorial F está relacionada à tendência do campo F de produzir rotação naquele ponto. Sabendo disso, considere o campo F(x,y,z) = (3x2)i + (x+y)j + (zx)k, encontre o seu rotacional, e assinale a alternativa correta: | |||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 9ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
| 10ª QUESTÃO | |||||||||||
. |
|||||||||||
| ALTERNATIVAS | |||||||||||
|
|||||||||||
 .
. .
. .
. .
. .
.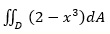 .
.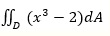 .
.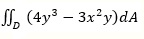 .
.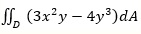 .
.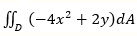 .
. .
.
 .
.

 .
.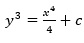 .
.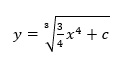 .
. .
. .
.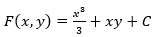 .
. .
. .
. .
. .
.